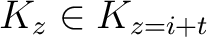MEA
Ein symmetrischer Blockverschlüsselungsalgorithmus
Michael Engel
|
Autor: |
Michael Engel |
|
|
Datum: |
06.04.2022
|
|
Der Blockverschlüsselungsalgorithmus MEA ist ein dynamischer symmetrischer Verschlüsseulgsalgorithmus. Er setzt auf ein dynamisches
Netzwerk und eine höhere Blockgröße als AES [#!AES:1!#], die die Sicherheit und den Algorithmus mit seiner größeren Blockgröße effizienter für 64-Bit CPUs macht. Der Algorithmus hat
eine dynamische SPN-ähnliche[#!AES:1!#] Struktur mit vergrößerten MDS-Matrizen und vier neue S-Boxen. Zudem werden verschiedenste Transformationen angewendet, damit es zur einer
besseren Obfuskation kommt. Die Schlüssellänge und die Blockgröße des Algorithmus sind äquivalent mit einer Größe von 512 Bits, was durch die Verminderung der Varietäten des Algorithmus zur einer Verminderung von
Schwachstellen führt. Außerdem wird eine neue Schlüsselerzeugung benutzt, die sehr schnell und effizient im Vergleich zu andern Schlüsselerzeugungen ist. Zudem wird ein Permutationsalgorithmus angewandt, der schnell und sicher eine
Permutation der Funktionen in Abhängigkeit vom Schlüssel erzeugt. Die Rundenanzahl vom MEA ist höher im Vergleich zu AES [#!AES:1!#], was die Sicherheit verbessern sollte.
Aktuell sind keine effizienten und effektiven Angriffe oder Schwachstellen vom MEA bekannt, weswegen MEA zur Zeit als sehr sicher einzustufen ist. Der Blockverschlüsselungsalgorithmus MEA ist auch
für Hardware-bassierte Aufgaben gedacht, da er leicht auf spezielle Hardware implementierbar ist. Die unten gegebene Implementierung ist auf Schnelligkeit ausgelegt, weswegen sie in der Programmiersprache C verfasst wurde.
Die follgenden Symbole und Definitionen werden benutzt im MEA.
| 0x |
- Prefix für Nummern im Hexadezimalsystem; |
|
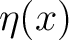 |
- das irreduzible Polynom
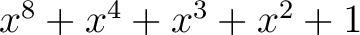 ; ; |
|
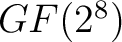 |
- ein endlicher Körper mit dem irreduziblen Polynom 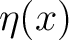 ; ; |
|
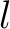 |
- die Blockgröße vom MEA, 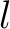 = 512; = 512; |
|
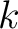 |
- die Schlüsselgröße vom MEA, 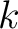 = 512; = 512; |
|
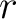 |
- die Anzahl der Reihen in der State-Matrix,
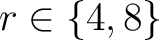 ; ; |
|
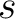 |
- die Anzahl der Spalten in der State-Matrix,
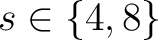 ; ; |
|
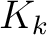 |
- der Schlüssel mit Länge 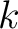 ; ; |
|
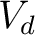 |
- d-Dimensionaler Vektorraum im 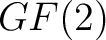 , , 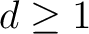 ; ; |
|
 |
- die binäre exklusiv ODER Verknüpfung; |
|
 |
- die rechts shift Operation mit einer konstanten Länge; |
|
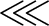 |
- die links shift Operation mit einer konstanten Länge; |
|
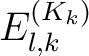 |
- die symmetrische Verschlüsselungstransformation, |
|
| |
dass mapping von
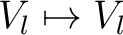 , abhängig von , abhängig von 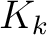 ; ; |
|
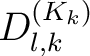 |
- die symmetrische Entschlüsselungstransformation, |
|
| |
dass mapping von
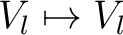 , abhängig von , abhängig von 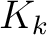 ; ; |
|
 |
- sequentieller Ablauf der der Transformationen 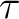 |
|
| |
und 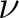 , ( , (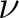 wird zuerst angewandt); wird zuerst angewandt); |
|
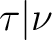 |
- Ablauf der Transformationen 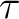 oder oder 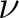 (jede wird einmal ausgeführt), (jede wird einmal ausgeführt), |
|
| |
Permutation generiert duch die Sequenz-Shuffle Funktion
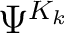 ; ; |
|
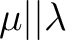 |
- Ablauf der Packete 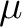 oder oder 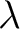 , , 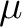 wird bei wird bei |
|
| |
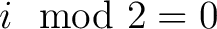 ausgeführt, abhängig von der Hauptrundenzahl ausgeführt, abhängig von der Hauptrundenzahl 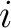 , , |
|
| |
ansonnsten wird 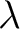 ausgeführt; ausgeführt; |
|
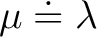 |
Substitution der Elemente
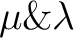 , ,
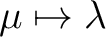 und und
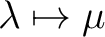 ; ; |
|
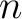 |
- die jeweilige Anzahl der Iterationen in den Transformationen |
|
| |
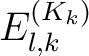 und und
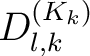 , , 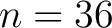 ; ; |
|
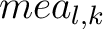 |
Applikation der Transformationen
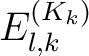 und und
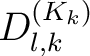 ; ; |
|
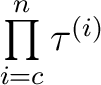 |
- sequentieller Ablauf der Transformationen
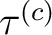 , , |
|
| |
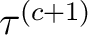 , ,
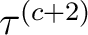 , ..., , ...,
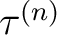 , ( , (
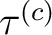 wird zuerst angewandt); wird zuerst angewandt); |
|
Die Verschlüsselungstransformation ist das mapping von
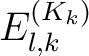 :
:
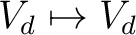 , dass
vom Schlüssel
, dass
vom Schlüssel 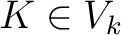 abhängig ist, wobei
abhängig ist, wobei 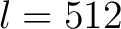 und
und 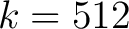 , also
, also 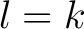 .
.
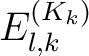 ist definiert
als eine Reihenfolge von
ist definiert
als eine Reihenfolge von 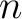 Paketen, jeweils bestehend aus
Paketen, jeweils bestehend aus 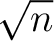 Funktionen, wobei bei
Funktionen, wobei bei
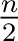 Paketen,
falls
Paketen,
falls
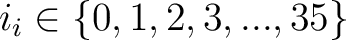 ,
,
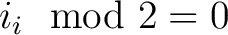 (die Rundenzahl), die Reihenfolge der Funktionen im Paket konstant ist. Ansonnsten ist bei
(die Rundenzahl), die Reihenfolge der Funktionen im Paket konstant ist. Ansonnsten ist bei
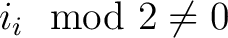 die Reihenfolge eine nicht vorhersehbare Permutation der
die Reihenfolge eine nicht vorhersehbare Permutation der 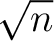 Funktionen in einem dynamischen Paket, die in Abhängigkeit von
Funktionen in einem dynamischen Paket, die in Abhängigkeit von 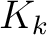 generiert wird.
Die jeweiligen Funktionen nehmen eine
generiert wird.
Die jeweiligen Funktionen nehmen eine 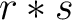 Matrix im
Matrix im 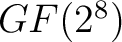 als Input, wobei
als Input, wobei 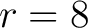 und
und 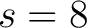 und
und 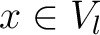 .
Die
.
Die 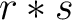 Matrix ist der Cihper State. Die Entschlüsselungstransformation
Matrix ist der Cihper State. Die Entschlüsselungstransformation
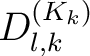 in Abhängigkeit von
in Abhängigkeit von 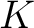 ist das inversive
mapping von
ist das inversive
mapping von
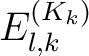 mit allen Inversiven der Funktionen.
mit allen Inversiven der Funktionen.
Alle Parameter, die 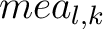 definieren, sind in Tabelle 1 angegeben.
definieren, sind in Tabelle 1 angegeben.
MEA
| Blockgröße |
Rundenanzahl |
Schlüssellänge |
Anzahl der Reihen |
Anzahl der Spalten |
|
|
|
|
|
|
|
|
| 512 |
36 |
512 |
8 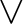 4 4 |
8 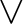 4 4 |
|
|
|
|
|
|
|
|
Die Transformationprozesse nehmen als Input einen Block der Länge 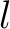 , egal ob bei der Verschlüsselung oder Entschlüsselung und geben
am Ende der Transformationen einen Block mit der Länge
, egal ob bei der Verschlüsselung oder Entschlüsselung und geben
am Ende der Transformationen einen Block mit der Länge 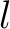 als Output. Die State-Matrix
als Output. Die State-Matrix 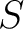 wird repräsentiert durch
wird repräsentiert durch
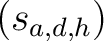 ,
wobei
,
wobei
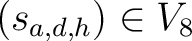 (bei
(bei
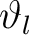 ,
, 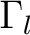 und
und
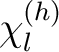 ) ,
) ,
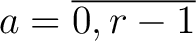 ,
,
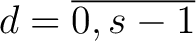 und falls
und falls
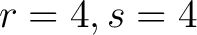 ist,
ist
ist,
ist
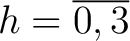 . Ansonnsten ist
. Ansonnsten ist 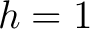 . Die State-Matrix wird befüllt mit den Input Bytes
. Die State-Matrix wird befüllt mit den Input Bytes
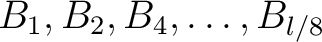 in der Row-Major Order,
dass heißt, dass als erstes die erste Reihe sequentiell von links nach rechts befüllt wird und danach die darunterliegende Reihe, bis
alle Reihen der Matrix voll sind. Falls die Input Nachricht
in der Row-Major Order,
dass heißt, dass als erstes die erste Reihe sequentiell von links nach rechts befüllt wird und danach die darunterliegende Reihe, bis
alle Reihen der Matrix voll sind. Falls die Input Nachricht
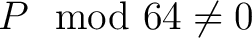 (in Bytes) ist, muss ein Padding Algorithmus
(in Bytes) ist, muss ein Padding Algorithmus![[*]](footnote.png) angewendet werden, damit die Nachricht in Bytes
angewendet werden, damit die Nachricht in Bytes
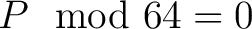 erfüllt.
erfüllt.
Der Verschlüsselungsalgortihmus
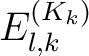 ist wie folgt definiert:
ist wie folgt definiert:
wo 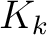 der Schlüssel mit der Länge
der Schlüssel mit der Länge 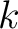 ist,
ist,
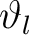 |
- die horizentale Permutation der Elemente
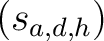 , wo , wo |
|
| |
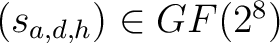 , ,
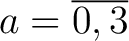 , ,
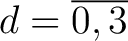 und und
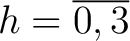 , mit dem , mit dem |
|
| |
Cipher-State 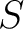 , , |
|
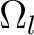 |
- das bijektive nicht lineare mapping der S-Boxen 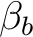 , ,
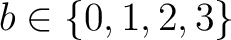 |
|
| |
mit den State-Matrix Vektoren, |
|
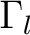 |
- die vertikale Permutation der Elemente
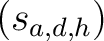 , wo , wo |
|
| |
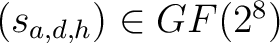 , ,
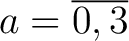 , ,
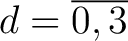 und und
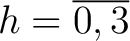 , mit dem , mit dem |
|
| |
Cipher-State 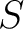 , , |
|
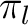 |
- die lineare Transformation des Cipher-State über das endliche Feld 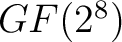 , , |
|
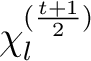 |
- die dimensionale Permutation der Elemente
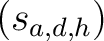 , wo , wo |
|
| |
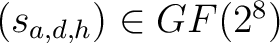 , ,
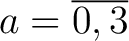 , ,
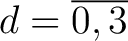 und und
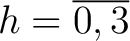 , mit dem , mit dem |
|
| |
Cipher-State 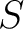 , bei , bei
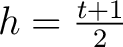 , , |
|
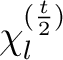 |
- die dimensionale Permutation der Elemente
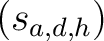 , wo , wo |
|
| |
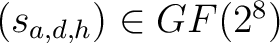 , ,
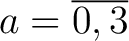 , ,
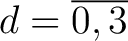 und und
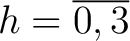 , mit dem , mit dem |
|
| |
Cipher-State 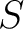 , bei , bei
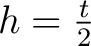 , , |
|
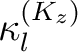 |
- eine Modulo 2 Addition (XOR-Operation) mit den Rundenschlüssel |
|
| |
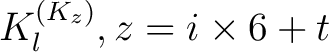 und mit der State-Matrix ist. und mit der State-Matrix ist. |
|
In den Funktionen
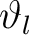 ,
, 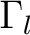 ,
,
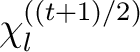 und
und
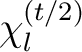 , mit dem Input
, mit dem Input 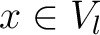 ,
werden die Permutationen in einer dreidimensionalen
,
werden die Permutationen in einer dreidimensionalen
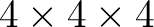 State-Matrix ausgeführt(
State-Matrix ausgeführt(
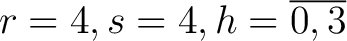 ), um eine bessere Obfuskation zu erziehlen.
Anonnsten wird immer eine zweidimensionale
), um eine bessere Obfuskation zu erziehlen.
Anonnsten wird immer eine zweidimensionale
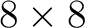 State-Matrix benutzt (
State-Matrix benutzt (
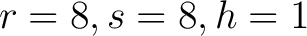 ). Als Rückgabe aller Funktionen wird eine zweidimensionale
). Als Rückgabe aller Funktionen wird eine zweidimensionale
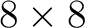 State-Matirx ausgegeben.
State-Matirx ausgegeben.
Die horizontale Permutation
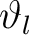 ist eine horizontale rechts shift Operation, die jede Reihe der drei dimensionalen State-Matrix
ist eine horizontale rechts shift Operation, die jede Reihe der drei dimensionalen State-Matrix
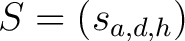 ,
,
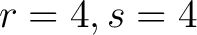 ,
,
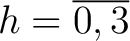 , um
, um 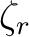 Positionen in einer Reihe
Positionen in einer Reihe 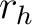 nach rechts bewegt.
nach rechts bewegt. 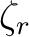 ist abhängig von der
Reihennummer
ist abhängig von der
Reihennummer
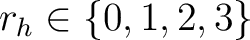 , die Blockgröße
, die Blockgröße 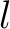 und kann mit der Formel
und kann mit der Formel
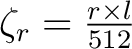 beschrieben werden. So wird
jede Reihe in jeder der vier Dimensionen um die Anzahl der Reihenzahl der Reihe nach rechts verschoben. So wird zum Beispiel jedes Element der Reihe
beschrieben werden. So wird
jede Reihe in jeder der vier Dimensionen um die Anzahl der Reihenzahl der Reihe nach rechts verschoben. So wird zum Beispiel jedes Element der Reihe 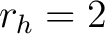 (in der dritten Reihe) um 2 Position nach rechts verschoben. Die Elemente, die rechts aus der Reihe gehen, werden wieder links angehangen. Dieser Prozess
wird für jeder der
(in der dritten Reihe) um 2 Position nach rechts verschoben. Die Elemente, die rechts aus der Reihe gehen, werden wieder links angehangen. Dieser Prozess
wird für jeder der
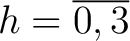 Dimensionen durchgeführt.
Dimensionen durchgeführt.
Ein Beispiel für die Dimension h = 0:
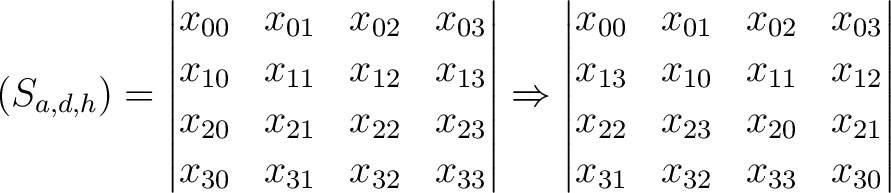
Die bijektive nicht lineare mapping Funktion 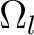 implementiert die S-Box Layer. Hier wird jedes Element
implementiert die S-Box Layer. Hier wird jedes Element
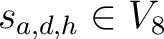 , wobei
, wobei
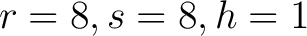 , der State-Matrix mit
, der State-Matrix mit
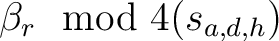 , wo
, wo
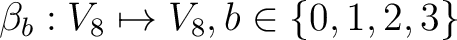 substituiert.
substituiert. 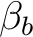 sind Substitutionsboxen, die unten angegeben sind. Zum Beispiel wird
sind Substitutionsboxen, die unten angegeben sind. Zum Beispiel wird
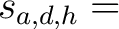 0x33 zu
0x33 zu
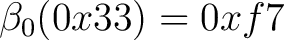 bei
bei 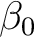 . Es können auch andere S-Boxen benutzt werden, solange sie sicher sind und in der beschriebenen Fuktionsweise funktionieren. Die
angegebenen S-Boxen
. Es können auch andere S-Boxen benutzt werden, solange sie sicher sind und in der beschriebenen Fuktionsweise funktionieren. Die
angegebenen S-Boxen 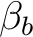 wurden mit Hilfe des Papers [#!SBOX:1!#] generiert.
wurden mit Hilfe des Papers [#!SBOX:1!#] generiert.
Die vertikale Permutation 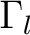 ist eine vertikale down shift Operation, die jede Spalte der drei dimensionalen State-Matrix
ist eine vertikale down shift Operation, die jede Spalte der drei dimensionalen State-Matrix
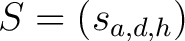 ,
,
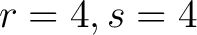 ,
,
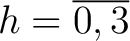 , um
, um 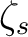 Positionen in einer Spalte
Positionen in einer Spalte 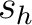 nach unten bewegt.
nach unten bewegt. 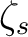 ist abhängig von der
Spaltennummer
ist abhängig von der
Spaltennummer
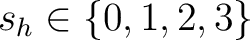 , die Blockgröße
, die Blockgröße 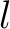 und kann mit der Formel
und kann mit der Formel
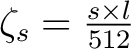 beschrieben werden.
Jede Spalte in jeder der vier Dimensionen wird um die Anzahl der der Spalten nach unten verschoben. So wird zum Beispiel jedes Element der Spalte
beschrieben werden.
Jede Spalte in jeder der vier Dimensionen wird um die Anzahl der der Spalten nach unten verschoben. So wird zum Beispiel jedes Element der Spalte 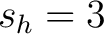 (in der vierten Spalte) um 3 Positionen nach unten verschoben. Die Elemente, die unten aus der Spalte gehen, werden wieder oben angehangen. Dieser Prozess
wird für jeder der
(in der vierten Spalte) um 3 Positionen nach unten verschoben. Die Elemente, die unten aus der Spalte gehen, werden wieder oben angehangen. Dieser Prozess
wird für jeder der
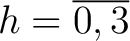 Dimensionen durchgeführt.
Dimensionen durchgeführt.
Ein Beispiel für die Dimension h = 0:
In der linearen Transformation 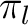 wird jedes Element
wird jedes Element
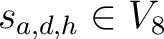 der State-Matrix
der State-Matrix 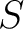 , wobei
, wobei
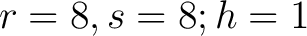 ist, als
ein Element des endlichen Feldes
ist, als
ein Element des endlichen Feldes 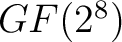 mit dem irreduziblen Polynom
mit dem irreduziblen Polynom
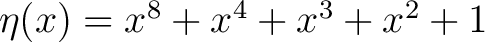 dargestellt. Jedes neue Element der neuen
resultierenden Matrix
dargestellt. Jedes neue Element der neuen
resultierenden Matrix
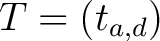 wird in dem
wird in dem 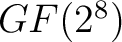 mit der folgenden Gleichung berechnet:
mit der folgenden Gleichung berechnet:
 ist hier die MDS-Matrix (maximum distance separable)
ist hier die MDS-Matrix (maximum distance separable)![[*]](footnote.png)
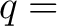 ( 0x08, 0x06, 0x07, 0x04, 0x01, 0x01, 0x05, 0x01), die eine Matrix ist, mit
bestimmten MDS Eigentschaften, die die Diffusion des Algorithmus stärkt.
( 0x08, 0x06, 0x07, 0x04, 0x01, 0x01, 0x05, 0x01), die eine Matrix ist, mit
bestimmten MDS Eigentschaften, die die Diffusion des Algorithmus stärkt. 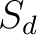 ist die d. Spalte der
ist die d. Spalte der 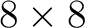 State-Matrix
State-Matrix
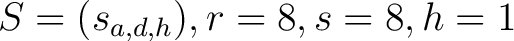 . Der Vektor
. Der Vektor 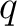 besteht
aus Elementen des endlichen Feldes
besteht
aus Elementen des endlichen Feldes 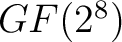 , die in jeder Reihe um
, die in jeder Reihe um 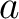 Einheiten, die Reihenzahl nach rechts verschoben werden. Am Ende der Transformation
Einheiten, die Reihenzahl nach rechts verschoben werden. Am Ende der Transformation 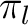 resultiert eine
neue
resultiert eine
neue 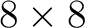 State-Matrix.
State-Matrix.
In der dimensionalen Permutation
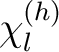 , abhängig vom Parameter
, abhängig vom Parameter
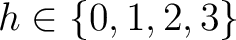 , wird die Dimension h in der
, wird die Dimension h in der
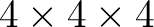 State-Matrix
State-Matrix
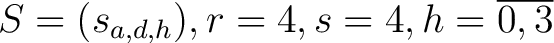 , einmal um 90 Grad nach links gedreht. So wird die Reihe
, einmal um 90 Grad nach links gedreht. So wird die Reihe 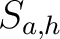 zur Spalte
zur Spalte
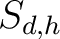 , wobei
, wobei 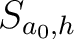 nach
nach 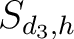 verschoben wird. Bei dem konstanten Packet
verschoben wird. Bei dem konstanten Packet 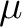 wird die Dimension
wird die Dimension 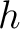 mit
mit
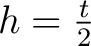 berechnet, bei der dann
die dimensionale Permutation angewendet wird. Bei dem variablen Packet
berechnet, bei der dann
die dimensionale Permutation angewendet wird. Bei dem variablen Packet 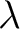 wird die Diemension
wird die Diemension 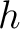 mit
mit
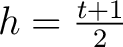 berechnet. Durch diese Gleichungen werden
nicht immer die gleichen Dimensionen im Cipher-State
berechnet. Durch diese Gleichungen werden
nicht immer die gleichen Dimensionen im Cipher-State 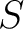 permutiert. Ein Beispiel für die Dimension
permutiert. Ein Beispiel für die Dimension 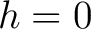 :
:
Die Funktion
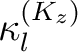 , welche abhänngig vom Parameter
, welche abhänngig vom Parameter
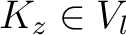 ist, hat als Argument die State-Matrix
ist, hat als Argument die State-Matrix 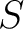 ,
, 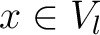 . Der Schlüssel
. Der Schlüssel 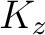 , wo
, wo
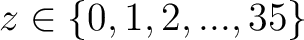 die aktuelle Runde ist, wird wie die State-Matrix
die aktuelle Runde ist, wird wie die State-Matrix 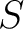 , in einer Matrix
der Größe
, in einer Matrix
der Größe 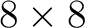 dargestellt. Dann wird der Schlüssel mit der State-Matrix mit Hilfe der XOR-Operation addiert. Das Ergebnis ist eine
State-Matrix der Größe
dargestellt. Dann wird der Schlüssel mit der State-Matrix mit Hilfe der XOR-Operation addiert. Das Ergebnis ist eine
State-Matrix der Größe 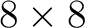 , mit der dann weitere Funktionen ausgeführt werden.
, mit der dann weitere Funktionen ausgeführt werden.
Der Entschlüsselungsalgortihmus
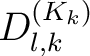 ist wie folgt definiert:
ist wie folgt definiert:
wo 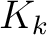 der Schlüssel mit der Länge
der Schlüssel mit der Länge 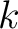 ist,
ist,
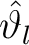 |
- die Inverse der horizentalen Permutation der Elemente
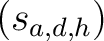 , wo , wo |
|
| |
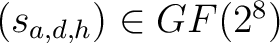 , ,
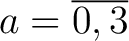 , ,
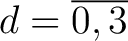 und und
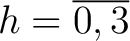 , mit dem , mit dem |
|
| |
Cipher-State 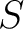 , , |
|
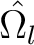 |
- das bijektive nicht lineare mapping der S-Boxen 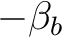 , ,
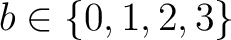 |
|
| |
mit den State-Matrix Vektoren, |
|
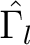 |
- die Inverse der vertikalen Permutation der Elemente
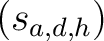 , wo , wo |
|
| |
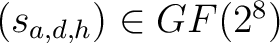 , ,
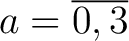 , ,
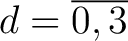 und und
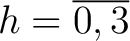 , mit dem , mit dem |
|
| |
dem Cipher-State 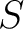 , , |
|
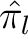 |
- die Inverse der linearen Transformation des Cipher-State über das |
|
| |
endliche Feld 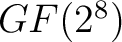 , , |
|
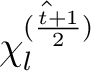 |
- die Inverse der dimensionalen Permutation der Elemente
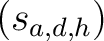 , wo , wo |
|
| |
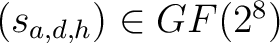 , ,
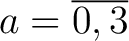 , ,
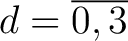 und und
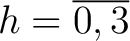 , mit dem , mit dem |
|
| |
Cipher-State 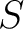 , bei , bei
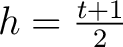 , , |
|
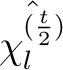 |
- die Inverse der dimensionalen Permutation der Elemente
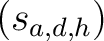 , wo , wo |
|
| |
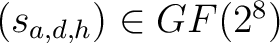 , ,
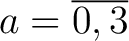 , ,
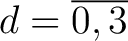 und und
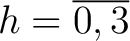 , mit dem , mit dem |
|
| |
Cipher-State 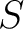 , bei , bei
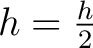 , , |
|
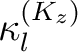 |
- eine Modulo 2 Addition (XOR-Operation) mit den Rundenschlüssel |
|
| |
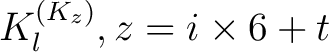 und mit der State-Matrix ist . und mit der State-Matrix ist . |
|
Wie bei der Verschlüsselung, wird bei den Funktionen
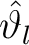 ,
,
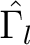 ,
,
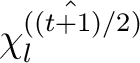 und
und
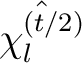 , mit dem Input
, mit dem Input 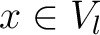 , die Inverse der Permutationen in einer dreidimensionalen
, die Inverse der Permutationen in einer dreidimensionalen
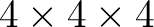 State-Matrix ausgeführt (
State-Matrix ausgeführt (
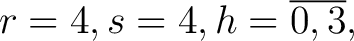 ), um eine bessere Obfuskation zu erzielen.
Ansonsten wird immer eine zweidimensionale
), um eine bessere Obfuskation zu erzielen.
Ansonsten wird immer eine zweidimensionale
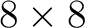 State-Matrix benutzt (
State-Matrix benutzt (
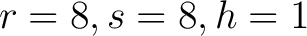 ). Als Rückgabe aller Funktionen wird eine zweidimensionale
). Als Rückgabe aller Funktionen wird eine zweidimensionale
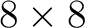 State-Matirx ausgegeben.
State-Matirx ausgegeben.
Die Inverse der horizontalen Permutation
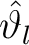 ist eine horizontale links shift Operation, die jede Reihe der drei dimensionalen State-Matrix
ist eine horizontale links shift Operation, die jede Reihe der drei dimensionalen State-Matrix
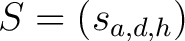 ,
,
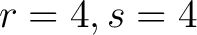 ,
,
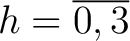 , um
, um 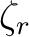 Positionen in einer Reihe
Positionen in einer Reihe 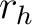 nach links bewegt.
nach links bewegt. 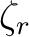 ist abhängig von der
Reihennummer
ist abhängig von der
Reihennummer
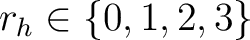 , die Blockgröße
, die Blockgröße 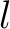 und kann mit der Formel
und kann mit der Formel
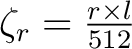 berechnet werden. So wird
jede Reihe in jeder der vier Dimensionen um die Anzahl der Reihenzahl der Reihe nach links verschoben. Zum Beispiel wird jedes Element der Reihe
berechnet werden. So wird
jede Reihe in jeder der vier Dimensionen um die Anzahl der Reihenzahl der Reihe nach links verschoben. Zum Beispiel wird jedes Element der Reihe 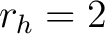 (in der dritten Reihe) um 2 Positionen nach links verschoben. Die Elemente, die links aus der Reihe gehen, werden wieder rechts angehangen. Dieser Prozess
wird für jeder der
(in der dritten Reihe) um 2 Positionen nach links verschoben. Die Elemente, die links aus der Reihe gehen, werden wieder rechts angehangen. Dieser Prozess
wird für jeder der
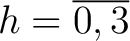 Dimensionen durchgeführt.
Dimensionen durchgeführt.
Ein Beispiel für die Dimension h = 0:
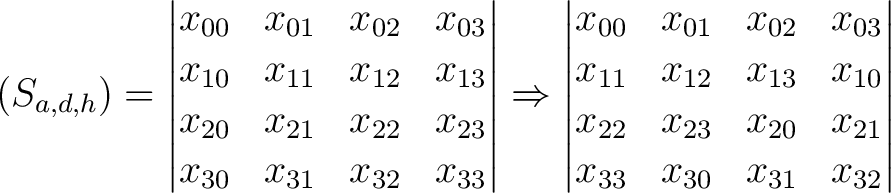
Die bijektive nicht lineare mapping Funktion
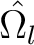 ist die Inverse der S-Box Layer. Hier wird jedes Element
ist die Inverse der S-Box Layer. Hier wird jedes Element
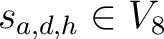 , wobei
, wobei
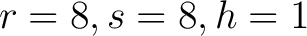 , der State-Matrix mit
, der State-Matrix mit
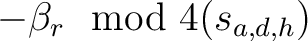 , wo
, wo
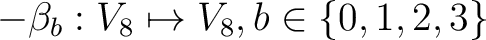 substituiert.
substituiert. 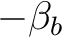 sind die inversen Substitutionsboxen, die unten angegeben sind. Zum Beispiel wird
sind die inversen Substitutionsboxen, die unten angegeben sind. Zum Beispiel wird
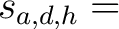 0xf7 zu
0xf7 zu
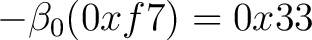 bei
bei 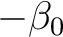 . Es können auch andere S-Boxen benutzt werden, solange sie die korrekten Inversen der S-Boxen sind.
. Es können auch andere S-Boxen benutzt werden, solange sie die korrekten Inversen der S-Boxen sind.
Die Inverse der vertikalen Permutation
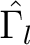 ist eine vertikale up shift Operation, die jede Spalte der drei dimensionalen State-Matrix
ist eine vertikale up shift Operation, die jede Spalte der drei dimensionalen State-Matrix
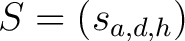 ,
,
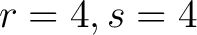 ,
,
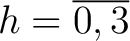 , um
, um 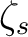 Positionen in einer Spalte
Positionen in einer Spalte 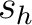 nach oben verschiebt.
nach oben verschiebt. 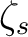 ist abhängig von der
Spaltennummer
ist abhängig von der
Spaltennummer
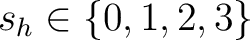 , die Blockgröße
, die Blockgröße 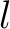 und kann mit der Formel
und kann mit der Formel
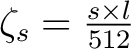 beschrieben werden. So wird
jede Spalte in jeder der drei Dimensionen um die Anzahl der Spaltenzahl der Spalten nach oben verschoben. Zum Beispiel wird jedes Element der Spalte
beschrieben werden. So wird
jede Spalte in jeder der drei Dimensionen um die Anzahl der Spaltenzahl der Spalten nach oben verschoben. Zum Beispiel wird jedes Element der Spalte 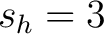 (in der vierten Spalte) um 3 Positionen nach oben verschoben. Die Elemente, die oben aus der Spalte gehen, werden wieder unten angehangen. Dieser Prozess
wird für jede der
(in der vierten Spalte) um 3 Positionen nach oben verschoben. Die Elemente, die oben aus der Spalte gehen, werden wieder unten angehangen. Dieser Prozess
wird für jede der
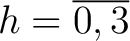 Dimensionen durchgeführt.
Dimensionen durchgeführt.
Ein Beispiel für die Dimension h = 0:
In der Inverse der linearen Transformation
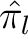 wird jedes Element
wird jedes Element
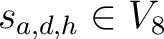 der State-Matrix
der State-Matrix 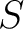 , wobei
, wobei
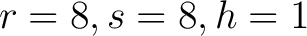 ist, als
ein Element des endlichen Feldes
ist, als
ein Element des endlichen Feldes 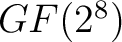 mit dem irreduziblen Polynom
mit dem irreduziblen Polynom
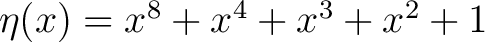 dargestellt. Jedes neue Element der neuen
resultierenden Matrix
dargestellt. Jedes neue Element der neuen
resultierenden Matrix
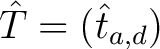 wird in dem
wird in dem 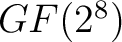 mit der folgenden Gleichung berechnet:
mit der folgenden Gleichung berechnet:
 ist hier die Inverse MDS-Matrix
ist hier die Inverse MDS-Matrix 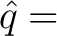 (0x2f,0x49,0xd7,0xca,0xad,0x95,0x76,0xa8), die auch die MDS Eigenschaften besitzt.
(0x2f,0x49,0xd7,0xca,0xad,0x95,0x76,0xa8), die auch die MDS Eigenschaften besitzt.
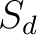 ist die d. Spalte der
ist die d. Spalte der 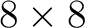 State-Matrix
State-Matrix
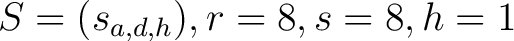 . Der Vektor
. Der Vektor 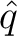 besteht
nur aus Elementen des endlichen Feldes
besteht
nur aus Elementen des endlichen Feldes 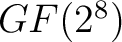 , die in jeder Reihe um
, die in jeder Reihe um 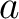 Einheiten, die Reihenzahl nach rechts verschoben werden. Am Ende der Inverse resultiert eine
neue
Einheiten, die Reihenzahl nach rechts verschoben werden. Am Ende der Inverse resultiert eine
neue 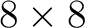 State-Matrix.
State-Matrix.
In der Inverse der dimensionalen Permutation
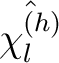 , abhängig vom Parameter
, abhängig vom Parameter
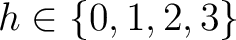 , wird die Dimension h in der
, wird die Dimension h in der
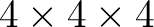 State-Matirx
State-Matirx
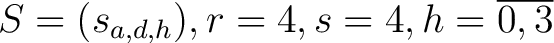 , zurück 90 Grad nach rechts gedreht. So wird wird die Spalte
, zurück 90 Grad nach rechts gedreht. So wird wird die Spalte 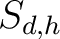 zur Reihe
zur Reihe
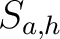 , wobei
, wobei 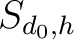 nach
nach 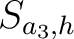 verschoben wird. Bei dem konstanten Packet
verschoben wird. Bei dem konstanten Packet 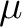 , wird die Dimension
, wird die Dimension 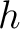 mit
mit
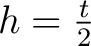 berechnet, bei der dann
die Inverse der dimensionalen Permutation angewendet wird. Bei den variablen Packeten
berechnet, bei der dann
die Inverse der dimensionalen Permutation angewendet wird. Bei den variablen Packeten 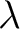 wird die Dimension
wird die Dimension 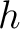 mit
mit
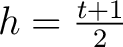 berechnet. Durch diese Gleichungen
wird die korrekte Inverse der dimensionalen Permutation berechnet. Ein Beispiel für die Dimension
berechnet. Durch diese Gleichungen
wird die korrekte Inverse der dimensionalen Permutation berechnet. Ein Beispiel für die Dimension 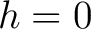 :
:
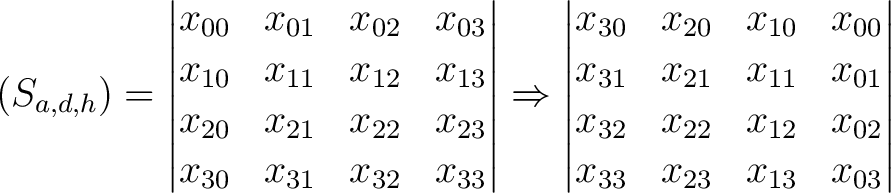
Die Rundenschlüssel
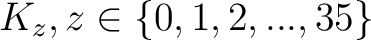 haben die gleiche Größe wie die Blocklänge
haben die gleiche Größe wie die Blocklänge 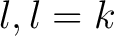 . In der Funktion
. In der Funktion
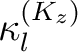 werden die Rundenschlüssel in der
werden die Rundenschlüssel in der 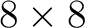 State-Matrix
State-Matrix 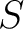 mit der XOR-Operation zusammenaddiert. Da es aber nicht sicher wäre, für jede Runde der
mit der XOR-Operation zusammenaddiert. Da es aber nicht sicher wäre, für jede Runde der 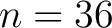 Runden den gleichen
Schlüssel zu benutzen, werden 36 Rundenschlüssel mit der folgenden Gleichung
Runden den gleichen
Schlüssel zu benutzen, werden 36 Rundenschlüssel mit der folgenden Gleichung 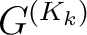 erzeugt.
erzeugt. 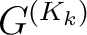 ist abhängig von dem Master-Schlüssel
ist abhängig von dem Master-Schlüssel
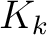 und von dem temporären Schlüssel
und von dem temporären Schlüssel 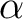 , der bei der ersten Runde
, der bei der ersten Runde
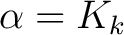 ist, und bei den restlichen 35 Schlüssel,
ist, und bei den restlichen 35 Schlüssel,
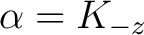 ist, wobei
ist, wobei 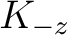 der vorherige Rundenschlüssl ist. Somit ist
der vorherige Rundenschlüssl ist. Somit ist 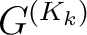 :
:
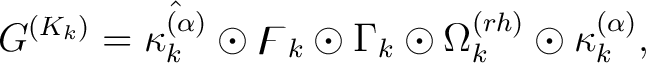
wo 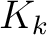 der Master-Schlüssel mit der Länge
der Master-Schlüssel mit der Länge 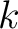 ist,
ist,
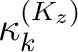 |
- eine Modulo 2 Addition (XOR-Operaton) mit dem Schlüssel 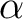 |
|
| |
und der RCON Konstanten 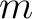 = 0xc6e8e5ed7b352d4 ist, = 0xc6e8e5ed7b352d4 ist, |
|
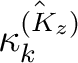 |
- eine Modulo 2 Addition (XOR-Operaton) mit dem Schlüssel 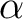 |
|
| |
und den Rundenschlüssel 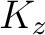 ist, ist, |
|
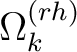 |
- das bijektive nicht lineare mapping der S-Boxen 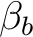 , ,
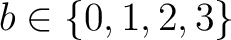 , mit der , mit der |
|
| |
konstanten Reihenfolge
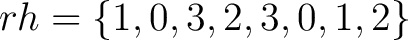 , statt einer sequenziellen , statt einer sequenziellen |
|
| |
Reihenfolge wie bei der Verschlüsselung, mit den Rundenschlüssel 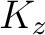 ist, ist, |
|
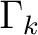 |
- die vertikale Permutation der Elemente
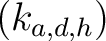 , wo , wo |
|
| |
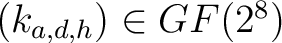 , ,
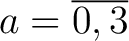 , ,
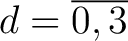 und und
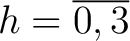 , mit dem , mit dem |
|
| |
Rundenschlüssel 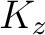 ist, ist, |
|
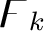 |
- die dimensionale Permutation der Elemente
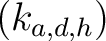 , wo , wo |
|
| |
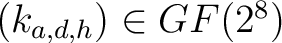 , ,
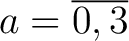 , ,
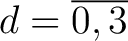 und und
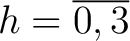 , mit dem , mit dem |
|
| |
Rundenschlüssel 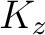 , hier aber die Dimensionen h in der Reihenfolge, , hier aber die Dimensionen h in der Reihenfolge, |
|
| |
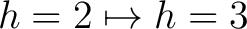 und und
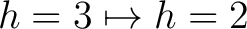 gewechselt wird. gewechselt wird. |
|
Die Funktion 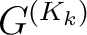 muss dann
muss dann 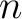 mal ausführt werden, damit man die benötigte Anzahl von Rundenschlüssel erzeugt. Es wurde
bewusst ein recht leicht zu berechnener Algorithmus für die Rundenschlüssel-Erzeugung entwickelt, da dieser Algorithmus auf die
nicht Vorhersehbarkeit des Master-Schlüssel
mal ausführt werden, damit man die benötigte Anzahl von Rundenschlüssel erzeugt. Es wurde
bewusst ein recht leicht zu berechnener Algorithmus für die Rundenschlüssel-Erzeugung entwickelt, da dieser Algorithmus auf die
nicht Vorhersehbarkeit des Master-Schlüssel 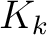 setzt und es somit nicht nötig und effizient wäre, einen komplexen Algorithmus für die
Rundenschlüssel-Erzeugung zu entwickeln und anzuwenden.
setzt und es somit nicht nötig und effizient wäre, einen komplexen Algorithmus für die
Rundenschlüssel-Erzeugung zu entwickeln und anzuwenden.
Da MEA nicht wie AES [#!AES:1!#] ein konstantes kryptographisches Netzwerk wie das SPN [#!AES:1!#] benutzt, muss eine dynamische Reihenfolge für jedes
dynamische Packet generiert werden. Diese Reihenfolge ist abhängig vom Schlüssel 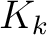 , doch sollte sie nicht vorhersehbar ohne den Schlüssel
, doch sollte sie nicht vorhersehbar ohne den Schlüssel
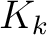 sein. Aus diesem Grund wird der Permutations Algorithmus
sein. Aus diesem Grund wird der Permutations Algorithmus
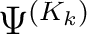 angewandt, der abhängig von den Rundenschlüsseln
angewandt, der abhängig von den Rundenschlüsseln 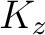 ist,
die vom Masterschlüssel
ist,
die vom Masterschlüssel 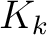 mit der vorher beschriebenen Funktion
mit der vorher beschriebenen Funktion 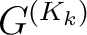 generiert wurden. Zuerst werden
generiert wurden. Zuerst werden
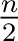 Arrays mit jeweils 6 Elementen
generiert, die jeweils sequentziell mit 0 bis 5 aufgefüllt werden. Dies ist die Startreihenfolge
Arrays mit jeweils 6 Elementen
generiert, die jeweils sequentziell mit 0 bis 5 aufgefüllt werden. Dies ist die Startreihenfolge
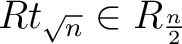 , wobei
, wobei
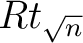 das t. Element von
das t. Element von
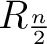 ist.
ist.
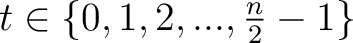 .
.
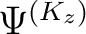 ist wie folgt definiert:
ist wie folgt definiert:
wobei
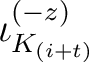 das x. Element von
das x. Element von
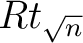 ist und mit Hilfe der Tabelle 2 in Ahbängigkeit vom Rundenschlüssel
ist und mit Hilfe der Tabelle 2 in Ahbängigkeit vom Rundenschlüssel 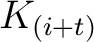 bestimmt wird. Bei der Funktion
bestimmt wird. Bei der Funktion
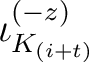 wird geschaut, ob die Nummer
wird geschaut, ob die Nummer
![$-y \in K_{[-z]}$](img189.png) , im Rundenschlüssel
, im Rundenschlüssel
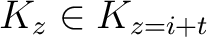 , kleiner als ein Wert ist und dann mit Hilfe der Tabelle 2 den größtmöglichen Wert zugewiesen wird. Das Resultat wird dann als Rückgabe gegeben.
, kleiner als ein Wert ist und dann mit Hilfe der Tabelle 2 den größtmöglichen Wert zugewiesen wird. Das Resultat wird dann als Rückgabe gegeben.
| Wert |
Resultat |
|
|
|
-y 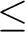 0x2A 0x2A |
0x00 |
|
|
|
-y 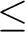 0x54 0x54 |
0x01 |
|
|
|
-y 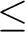 0x7E 0x7E |
0x02 |
|
|
|
-y 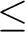 0xA8 0xA8 |
0x03 |
|
|
|
-y 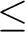 0xD2 0xD2 |
0x04 |
|
|
|
-y 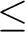 0xFF 0xFF |
0x05 |
|
|
|
| Wert |
Funktion |
|
|
|
| 0x00 |
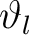 oder oder
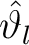 (bei (bei
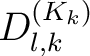 ) ) |
|
|
|
| 0x01 |
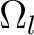 oder oder
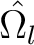 (bei (bei
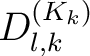 ) ) |
|
|
|
| 0x02 |
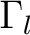 oder oder
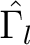 (bei (bei
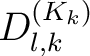 ) ) |
|
|
|
| 0x03 |
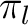 oder oder
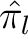 (bei (bei
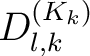 ) ) |
|
|
|
| 0x04 |
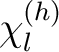 oder oder
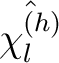 (bei (bei
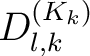 ) ) |
|
|
|
| 0x05 |
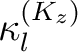 |
|
|
|
Tabelle 2 und Tabelle 3
Dieser Prozess wird dann 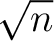 -mal wiederholt, damit eine sichere Permutation ensteht. Diese Permutation wird dann als
dynamische Reihenfolge
-mal wiederholt, damit eine sichere Permutation ensteht. Diese Permutation wird dann als
dynamische Reihenfolge
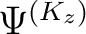 benutzt, die mit Hilfe der Tabelle 3 die jeweligen Funktionen in
benutzt, die mit Hilfe der Tabelle 3 die jeweligen Funktionen in
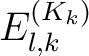 und
und
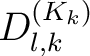 ausführt.
ausführt.
Die 8 Substitutionsboxen sind wie folgt definiert:
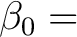
{
0xce, 0xbb, 0xeb, 0x92, 0xea, 0xcb, 0x13, 0xc1,
0xe9, 0x3a, 0xd6, 0xb2, 0xd2, 0x90, 0x17, 0xf8,
0x42, 0x15, 0x56, 0xb4, 0x65, 0x1c, 0x88, 0x43,
0xc5, 0x5c, 0x36, 0xba, 0xf5, 0x57, 0x67, 0x8d,
0x31, 0xf6, 0x64, 0x58, 0x9e, 0xf4, 0x22, 0xaa,
0x75, 0x0f, 0x02, 0xb1, 0xdf, 0x6d, 0x73, 0x4d,
0x7c, 0x26, 0x2e, 0xf7, 0x08, 0x5d, 0x44, 0x3e,
0x9f, 0x14, 0xc8, 0xae, 0x54, 0x10, 0xd8, 0xbc,
0x1a, 0x6b, 0x69, 0xf3, 0xbd, 0x33, 0xab, 0xfa,
0xd1, 0x9b, 0x68, 0x4e, 0x16, 0x95, 0x91, 0xee,
0x4c, 0x63, 0x8e, 0x5b, 0xcc, 0x3c, 0x19, 0xa1,
0x81, 0x49, 0x7b, 0xd9, 0x6f, 0x37, 0x60, 0xca,
0xe7, 0x2b, 0x48, 0xfd, 0x96, 0x45, 0xfc, 0x41,
0x12, 0x0d, 0x79, 0xe5, 0x89, 0x8c, 0xe3, 0x20,
0x30, 0xdc, 0xb7, 0x6c, 0x4a, 0xb5, 0x3f, 0x97,
0xd4, 0x62, 0x2d, 0x06, 0xa4, 0xa5, 0x83, 0x5f,
0x2a, 0xda, 0xc9, 0x00, 0x7e, 0xa2, 0x55, 0xbf,
0x11, 0xd5, 0x9c, 0xcf, 0x0e, 0x0a, 0x3d, 0x51,
0x7d, 0x93, 0x1b, 0xfe, 0xc4, 0x47, 0x09, 0x86,
0x0b, 0x8f, 0x9d, 0x6a, 0x07, 0xb9, 0xb0, 0x98,
0x18, 0x32, 0x71, 0x4b, 0xef, 0x3b, 0x70, 0xa0,
0xe4, 0x40, 0xff, 0xc3, 0xa9, 0xe6, 0x78, 0xf9,
0x8b, 0x46, 0x80, 0x1e, 0x38, 0xe1, 0xb8, 0xa8,
0xe0, 0x0c, 0x23, 0x76, 0x1d, 0x25, 0x24, 0x05,
0xf1, 0x6e, 0x94, 0x28, 0x9a, 0x84, 0xe8, 0xa3,
0x4f, 0x77, 0xd3, 0x85, 0xe2, 0x52, 0xf2, 0x82,
0x50, 0x7a, 0x2f, 0x74, 0x53, 0xb3, 0x61, 0xaf,
0x39, 0x35, 0xde, 0xcd, 0x1f, 0x99, 0xac, 0xad,
0x72, 0x2c, 0xdd, 0xd0, 0x87, 0xbe, 0x5e, 0xa6,
0xec, 0x04, 0xc6, 0x03, 0x34, 0xfb, 0xdb, 0x59,
0xb6, 0xc2, 0x01, 0xf0, 0x5a, 0xed, 0xa7, 0x66,
0x21, 0x7f, 0x8a, 0x27, 0xc7, 0xc0, 0x29, 0xd7
}
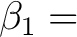
{
0x14, 0x9d, 0xb9, 0xe7, 0x67, 0x4c, 0x50, 0x82,
0xca, 0xe5, 0x1d, 0x31, 0x0a, 0xc6, 0xb2, 0x51,
0xa2, 0xd8, 0x54, 0x90, 0xd0, 0xce, 0x2d, 0x7d,
0xc7, 0x7e, 0xd7, 0x94, 0xdf, 0x83, 0x8e, 0x6c,
0x66, 0xd2, 0x6f, 0x16, 0x1e, 0x76, 0xfe, 0xcc,
0xaa, 0x5a, 0x8f, 0x17, 0xbd, 0x2c, 0xac, 0xea,
0x7b, 0x65, 0xa9, 0x10, 0xc0, 0x92, 0xee, 0xbe,
0x6a, 0x6e, 0x48, 0x96, 0x95, 0xe9, 0x32, 0xbc,
0xa1, 0x42, 0xd5, 0xa7, 0x81, 0xb4, 0x5f, 0xe6,
0xc2, 0x5d, 0xad, 0x3a, 0xb7, 0x0c, 0x8d, 0x01,
0x98, 0xfd, 0x12, 0x02, 0x75, 0x13, 0x0f, 0x6b,
0x22, 0xe2, 0xab, 0xf7, 0x7f, 0xba, 0x97, 0xd1,
0x64, 0xd9, 0xc4, 0x59, 0xaf, 0x23, 0x33, 0x37,
0xde, 0xae, 0x60, 0x05, 0x63, 0xa8, 0x52, 0xa5,
0x4e, 0xe0, 0xdd, 0x71, 0xf2, 0x24, 0x34, 0x57,
0x47, 0xa4, 0xb3, 0x9e, 0x2f, 0xc1, 0xb8, 0xcb,
0x2b, 0xd4, 0x0d, 0x36, 0x91, 0x8b, 0x9c, 0x26,
0x25, 0x61, 0xa3, 0xd6, 0xeb, 0x35, 0x53, 0xf4,
0x2e, 0x88, 0x80, 0xe4, 0x30, 0xdb, 0xfc, 0x0e,
0x77, 0x8c, 0x93, 0xa6, 0x78, 0x06, 0xe1, 0xec,
0xf9, 0x03, 0xa0, 0x27, 0xda, 0xef, 0x5c, 0x00,
0x7a, 0x45, 0xe8, 0x40, 0x1a, 0x4b, 0x5e, 0x73,
0xc3, 0xff, 0xf5, 0xf3, 0xb0, 0xc5, 0x49, 0x21,
0xfa, 0x11, 0x39, 0x84, 0x43, 0x38, 0x85, 0x07,
0xf0, 0x79, 0x46, 0xf8, 0xe3, 0x1f, 0x09, 0xb6,
0xcd, 0x55, 0x1c, 0x1b, 0xfb, 0x7c, 0xed, 0x6d,
0x15, 0x56, 0x86, 0x20, 0x68, 0x4a, 0x41, 0x4f,
0xd3, 0x99, 0x08, 0xf6, 0x3f, 0x89, 0x62, 0x04,
0xcf, 0xc8, 0x69, 0x9f, 0x19, 0x5b, 0x44, 0x9b,
0x87, 0xb1, 0x3d, 0xbb, 0xdc, 0x2a, 0xbf, 0x58,
0x3c, 0x8a, 0x18, 0x3e, 0x72, 0x0b, 0x28, 0x4d,
0xb5, 0x9a, 0xc9, 0x74, 0x29, 0xf1, 0x3b, 0x70
}
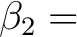
{
0x68, 0x8d, 0xca, 0x4d, 0x73, 0x4b, 0x4e, 0x2a,
0xd4, 0x52, 0x26, 0xb3, 0x54, 0x1e, 0x19, 0x1f,
0x22, 0x03, 0x46, 0x3d, 0x2d, 0x4a, 0x53, 0x83,
0x13, 0x8a, 0xb7, 0xd5, 0x25, 0x79, 0xf5, 0xbd,
0x58, 0x2f, 0x0d, 0x02, 0xed, 0x51, 0x9e, 0x11,
0xf2, 0x3e, 0x55, 0x5e, 0xd1, 0x16, 0x3c, 0x66,
0x70, 0x5d, 0xf3, 0x45, 0x40, 0xcc, 0xe8, 0x94,
0x56, 0x08, 0xce, 0x1a, 0x3a, 0xd2, 0xe1, 0xdf,
0xb5, 0x38, 0x6e, 0x0e, 0xe5, 0xf4, 0xf9, 0x86,
0xe9, 0x4f, 0xd6, 0x85, 0x23, 0xcf, 0x32, 0x99,
0x31, 0x14, 0xae, 0xee, 0xc8, 0x48, 0xd3, 0x30,
0xa1, 0x92, 0x41, 0xb1, 0x18, 0xc4, 0x2c, 0x71,
0x72, 0x44, 0x15, 0xfd, 0x37, 0xbe, 0x5f, 0xaa,
0x9b, 0x88, 0xd8, 0xab, 0x89, 0x9c, 0xfa, 0x60,
0xea, 0xbc, 0x62, 0x0c, 0x24, 0xa6, 0xa8, 0xec,
0x67, 0x20, 0xdb, 0x7c, 0x28, 0xdd, 0xac, 0x5b,
0x34, 0x7e, 0x10, 0xf1, 0x7b, 0x8f, 0x63, 0xa0,
0x05, 0x9a, 0x43, 0x77, 0x21, 0xbf, 0x27, 0x09,
0xc3, 0x9f, 0xb6, 0xd7, 0x29, 0xc2, 0xeb, 0xc0,
0xa4, 0x8b, 0x8c, 0x1d, 0xfb, 0xff, 0xc1, 0xb2,
0x97, 0x2e, 0xf8, 0x65, 0xf6, 0x75, 0x07, 0x04,
0x49, 0x33, 0xe4, 0xd9, 0xb9, 0xd0, 0x42, 0xc7,
0x6c, 0x90, 0x00, 0x8e, 0x6f, 0x50, 0x01, 0xc5,
0xda, 0x47, 0x3f, 0xcd, 0x69, 0xa2, 0xe2, 0x7a,
0xa7, 0xc6, 0x93, 0x0f, 0x0a, 0x06, 0xe6, 0x2b,
0x96, 0xa3, 0x1c, 0xaf, 0x6a, 0x12, 0x84, 0x39,
0xe7, 0xb0, 0x82, 0xf7, 0xfe, 0x9d, 0x87, 0x5c,
0x81, 0x35, 0xde, 0xb4, 0xa5, 0xfc, 0x80, 0xef,
0xcb, 0xbb, 0x6b, 0x76, 0xba, 0x5a, 0x7d, 0x78,
0x0b, 0x95, 0xe3, 0xad, 0x74, 0x98, 0x3b, 0x36,
0x64, 0x6d, 0xdc, 0xf0, 0x59, 0xa9, 0x4c, 0x17,
0x7f, 0x91, 0xb8, 0xc9, 0x57, 0x1b, 0xe0, 0x61
}
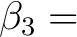
{
0xa8, 0x43, 0x5f, 0x06, 0x6b, 0x75, 0x6c, 0x59,
0x71, 0xdf, 0x87, 0x95, 0x17, 0xf0, 0xd8, 0x09,
0x6d, 0xf3, 0x1d, 0xcb, 0xc9, 0x4d, 0x2c, 0xaf,
0x79, 0xe0, 0x97, 0xfd, 0x6f, 0x4b, 0x45, 0x39,
0x3e, 0xdd, 0xa3, 0x4f, 0xb4, 0xb6, 0x9a, 0x0e,
0x1f, 0xbf, 0x15, 0xe1, 0x49, 0xd2, 0x93, 0xc6,
0x92, 0x72, 0x9e, 0x61, 0xd1, 0x63, 0xfa, 0xee,
0xf4, 0x19, 0xd5, 0xad, 0x58, 0xa4, 0xbb, 0xa1,
0xdc, 0xf2, 0x83, 0x37, 0x42, 0xe4, 0x7a, 0x32,
0x9c, 0xcc, 0xab, 0x4a, 0x8f, 0x6e, 0x04, 0x27,
0x2e, 0xe7, 0xe2, 0x5a, 0x96, 0x16, 0x23, 0x2b,
0xc2, 0x65, 0x66, 0x0f, 0xbc, 0xa9, 0x47, 0x41,
0x34, 0x48, 0xfc, 0xb7, 0x6a, 0x88, 0xa5, 0x53,
0x86, 0xf9, 0x5b, 0xdb, 0x38, 0x7b, 0xc3, 0x1e,
0x22, 0x33, 0x24, 0x28, 0x36, 0xc7, 0xb2, 0x3b,
0x8e, 0x77, 0xba, 0xf5, 0x14, 0x9f, 0x08, 0x55,
0x9b, 0x4c, 0xfe, 0x60, 0x5c, 0xda, 0x18, 0x46,
0xcd, 0x7d, 0x21, 0xb0, 0x3f, 0x1b, 0x89, 0xff,
0xeb, 0x84, 0x69, 0x3a, 0x9d, 0xd7, 0xd3, 0x70,
0x67, 0x40, 0xb5, 0xde, 0x5d, 0x30, 0x91, 0xb1,
0x78, 0x11, 0x01, 0xe5, 0x00, 0x68, 0x98, 0xa0,
0xc5, 0x02, 0xa6, 0x74, 0x2d, 0x0b, 0xa2, 0x76,
0xb3, 0xbe, 0xce, 0xbd, 0xae, 0xe9, 0x8a, 0x31,
0x1c, 0xec, 0xf1, 0x99, 0x94, 0xaa, 0xf6, 0x26,
0x2f, 0xef, 0xe8, 0x8c, 0x35, 0x03, 0xd4, 0x7f,
0xfb, 0x05, 0xc1, 0x5e, 0x90, 0x20, 0x3d, 0x82,
0xf7, 0xea, 0x0a, 0x0d, 0x7e, 0xf8, 0x50, 0x1a,
0xc4, 0x07, 0x57, 0xb8, 0x3c, 0x62, 0xe3, 0xc8,
0xac, 0x52, 0x64, 0x10, 0xd0, 0xd9, 0x13, 0x0c,
0x12, 0x29, 0x51, 0xb9, 0xcf, 0xd6, 0x73, 0x8d,
0x81, 0x54, 0xc0, 0xed, 0x4e, 0x44, 0xa7, 0x2a,
0x85, 0x25, 0xe6, 0xca, 0x7c, 0x8b, 0x56, 0x80
}
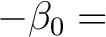
{
0x83, 0xf2, 0x2a, 0xeb, 0xe9, 0xbf, 0x7b, 0x9c,
0x34, 0x96, 0x8d, 0x98, 0xb9, 0x69, 0x8c, 0x29,
0x3d, 0x88, 0x68, 0x06, 0x39, 0x11, 0x4c, 0x0e,
0xa0, 0x56, 0x40, 0x92, 0x15, 0xbc, 0xb3, 0xdc,
0x6f, 0xf8, 0x26, 0xba, 0xbe, 0xbd, 0x31, 0xfb,
0xc3, 0xfe, 0x80, 0x61, 0xe1, 0x7a, 0x32, 0xd2,
0x70, 0x20, 0xa1, 0x45, 0xec, 0xd9, 0x1a, 0x5d,
0xb4, 0xd8, 0x09, 0xa5, 0x55, 0x8e, 0x37, 0x76,
0xa9, 0x67, 0x10, 0x17, 0x36, 0x65, 0xb1, 0x95,
0x62, 0x59, 0x74, 0xa3, 0x50, 0x2f, 0x4b, 0xc8,
0xd0, 0x8f, 0xcd, 0xd4, 0x3c, 0x86, 0x12, 0x1d,
0x23, 0xef, 0xf4, 0x53, 0x19, 0x35, 0xe6, 0x7f,
0x5e, 0xd6, 0x79, 0x51, 0x22, 0x14, 0xf7, 0x1e,
0x4a, 0x42, 0x9b, 0x41, 0x73, 0x2d, 0xc1, 0x5c,
0xa6, 0xa2, 0xe0, 0x2e, 0xd3, 0x28, 0xbb, 0xc9,
0xae, 0x6a, 0xd1, 0x5a, 0x30, 0x90, 0x84, 0xf9,
0xb2, 0x58, 0xcf, 0x7e, 0xc5, 0xcb, 0x97, 0xe4,
0x16, 0x6c, 0xfa, 0xb0, 0x6d, 0x1f, 0x52, 0x99,
0x0d, 0x4e, 0x03, 0x91, 0xc2, 0x4d, 0x64, 0x77,
0x9f, 0xdd, 0xc4, 0x49, 0x8a, 0x9a, 0x24, 0x38,
0xa7, 0x57, 0x85, 0xc7, 0x7c, 0x7d, 0xe7, 0xf6,
0xb7, 0xac, 0x27, 0x46, 0xde, 0xdf, 0x3b, 0xd7,
0x9e, 0x2b, 0x0b, 0xd5, 0x13, 0x75, 0xf0, 0x72,
0xb6, 0x9d, 0x1b, 0x01, 0x3f, 0x44, 0xe5, 0x87,
0xfd, 0x07, 0xf1, 0xab, 0x94, 0x18, 0xea, 0xfc,
0x3a, 0x82, 0x5f, 0x05, 0x54, 0xdb, 0x00, 0x8b,
0xe3, 0x48, 0x0c, 0xca, 0x78, 0x89, 0x0a, 0xff,
0x3e, 0x5b, 0x81, 0xee, 0x71, 0xe2, 0xda, 0x2c,
0xb8, 0xb5, 0xcc, 0x6e, 0xa8, 0x6b, 0xad, 0x60,
0xc6, 0x08, 0x04, 0x02, 0xe8, 0xf5, 0x4f, 0xa4,
0xf3, 0xc0, 0xce, 0x43, 0x25, 0x1c, 0x21, 0x33,
0x0f, 0xaf, 0x47, 0xed, 0x66, 0x63, 0x93, 0xaa
}
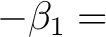
{
0xa7, 0x4f, 0x53, 0xa1, 0xdf, 0x6b, 0x9d, 0xbf,
0xda, 0xc6, 0x0c, 0xf5, 0x4d, 0x82, 0x97, 0x56,
0x33, 0xb9, 0x52, 0x55, 0x00, 0xd0, 0x23, 0x2b,
0xf2, 0xe4, 0xac, 0xcb, 0xca, 0x0a, 0x24, 0xc5,
0xd3, 0xb7, 0x58, 0x65, 0x75, 0x88, 0x87, 0xa3,
0xf6, 0xfc, 0xed, 0x80, 0x2d, 0x16, 0x90, 0x7c,
0x94, 0x0b, 0x3e, 0x66, 0x76, 0x8d, 0x83, 0x67,
0xbd, 0xba, 0x4b, 0xfe, 0xf0, 0xea, 0xf3, 0xdc,
0xab, 0xd6, 0x41, 0xbc, 0xe6, 0xa9, 0xc2, 0x78,
0x3a, 0xb6, 0xd5, 0xad, 0x05, 0xf7, 0x70, 0xd7,
0x06, 0x0f, 0x6e, 0x8e, 0x12, 0xc9, 0xd1, 0x77,
0xef, 0x63, 0x29, 0xe5, 0xa6, 0x49, 0xae, 0x46,
0x6a, 0x89, 0xde, 0x6c, 0x60, 0x31, 0x20, 0x04,
0xd4, 0xe2, 0x38, 0x57, 0x1f, 0xcf, 0x39, 0x22,
0xff, 0x73, 0xf4, 0xaf, 0xfb, 0x54, 0x25, 0x98,
0x9c, 0xc1, 0xa8, 0x30, 0xcd, 0x17, 0x19, 0x5c,
0x92, 0x44, 0x07, 0x1d, 0xbb, 0xbe, 0xd2, 0xe8,
0x91, 0xdd, 0xf1, 0x85, 0x99, 0x4e, 0x1e, 0x2a,
0x13, 0x84, 0x35, 0x9a, 0x1b, 0x3c, 0x3b, 0x5e,
0x50, 0xd9, 0xf9, 0xe7, 0x86, 0x01, 0x7b, 0xe3,
0xa2, 0x40, 0x10, 0x8a, 0x79, 0x6f, 0x9b, 0x43,
0x6d, 0x32, 0x28, 0x5a, 0x2e, 0x4a, 0x69, 0x64,
0xb4, 0xe9, 0x0e, 0x7a, 0x45, 0xf8, 0xc7, 0x4c,
0x7e, 0x02, 0x5d, 0xeb, 0x3f, 0x2c, 0x37, 0xee,
0x34, 0x7d, 0x48, 0xb0, 0x62, 0xb5, 0x0d, 0x18,
0xe1, 0xfa, 0x08, 0x7f, 0x27, 0xc8, 0x15, 0xe0,
0x14, 0x5f, 0x21, 0xd8, 0x81, 0x42, 0x8b, 0x1a,
0x11, 0x61, 0xa4, 0x95, 0xec, 0x72, 0x68, 0x1c,
0x71, 0x9e, 0x59, 0xc4, 0x93, 0x09, 0x47, 0x03,
0xaa, 0x3d, 0x2f, 0x8c, 0x9f, 0xce, 0x36, 0xa5,
0xc0, 0xfd, 0x74, 0xb3, 0x8f, 0xb2, 0xdb, 0x5b,
0xc3, 0xa0, 0xb8, 0xcc, 0x96, 0x51, 0x26, 0xb1
}
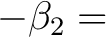
{
0xb2, 0xb6, 0x23, 0x11, 0xa7, 0x88, 0xc5, 0xa6,
0x39, 0x8f, 0xc4, 0xe8, 0x73, 0x22, 0x43, 0xc3,
0x82, 0x27, 0xcd, 0x18, 0x51, 0x62, 0x2d, 0xf7,
0x5c, 0x0e, 0x3b, 0xfd, 0xca, 0x9b, 0x0d, 0x0f,
0x79, 0x8c, 0x10, 0x4c, 0x74, 0x1c, 0x0a, 0x8e,
0x7c, 0x94, 0x07, 0xc7, 0x5e, 0x14, 0xa1, 0x21,
0x57, 0x50, 0x4e, 0xa9, 0x80, 0xd9, 0xef, 0x64,
0x41, 0xcf, 0x3c, 0xee, 0x2e, 0x13, 0x29, 0xba,
0x34, 0x5a, 0xae, 0x8a, 0x61, 0x33, 0x12, 0xb9,
0x55, 0xa8, 0x15, 0x05, 0xf6, 0x03, 0x06, 0x49,
0xb5, 0x25, 0x09, 0x16, 0x0c, 0x2a, 0x38, 0xfc,
0x20, 0xf4, 0xe5, 0x7f, 0xd7, 0x31, 0x2b, 0x66,
0x6f, 0xff, 0x72, 0x86, 0xf0, 0xa3, 0x2f, 0x78,
0x00, 0xbc, 0xcc, 0xe2, 0xb0, 0xf1, 0x42, 0xb4,
0x30, 0x5f, 0x60, 0x04, 0xec, 0xa5, 0xe3, 0x8b,
0xe7, 0x1d, 0xbf, 0x84, 0x7b, 0xe6, 0x81, 0xf8,
0xde, 0xd8, 0xd2, 0x17, 0xce, 0x4b, 0x47, 0xd6,
0x69, 0x6c, 0x19, 0x99, 0x9a, 0x01, 0xb3, 0x85,
0xb1, 0xf9, 0x59, 0xc2, 0x37, 0xe9, 0xc8, 0xa0,
0xed, 0x4f, 0x89, 0x68, 0x6d, 0xd5, 0x26, 0x91,
0x87, 0x58, 0xbd, 0xc9, 0x98, 0xdc, 0x75, 0xc0,
0x76, 0xf5, 0x67, 0x6b, 0x7e, 0xeb, 0x52, 0xcb,
0xd1, 0x5b, 0x9f, 0x0b, 0xdb, 0x40, 0x92, 0x1a,
0xfa, 0xac, 0xe4, 0xe1, 0x71, 0x1f, 0x65, 0x8d,
0x97, 0x9e, 0x95, 0x90, 0x5d, 0xb7, 0xc1, 0xaf,
0x54, 0xfb, 0x02, 0xe0, 0x35, 0xbb, 0x3a, 0x4d,
0xad, 0x2c, 0x3d, 0x56, 0x08, 0x1b, 0x4a, 0x93,
0x6a, 0xab, 0xb8, 0x7a, 0xf2, 0x7d, 0xda, 0x3f,
0xfe, 0x3e, 0xbe, 0xea, 0xaa, 0x44, 0xc6, 0xd0,
0x36, 0x48, 0x70, 0x96, 0x77, 0x24, 0x53, 0xdf,
0xf3, 0x83, 0x28, 0x32, 0x45, 0x1e, 0xa4, 0xd3,
0xa2, 0x46, 0x6e, 0x9c, 0xdd, 0x63, 0xd4, 0x9d
}
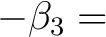
{
0xa4, 0xa2, 0xa9, 0xc5, 0x4e, 0xc9, 0x03, 0xd9,
0x7e, 0x0f, 0xd2, 0xad, 0xe7, 0xd3, 0x27, 0x5b,
0xe3, 0xa1, 0xe8, 0xe6, 0x7c, 0x2a, 0x55, 0x0c,
0x86, 0x39, 0xd7, 0x8d, 0xb8, 0x12, 0x6f, 0x28,
0xcd, 0x8a, 0x70, 0x56, 0x72, 0xf9, 0xbf, 0x4f,
0x73, 0xe9, 0xf7, 0x57, 0x16, 0xac, 0x50, 0xc0,
0x9d, 0xb7, 0x47, 0x71, 0x60, 0xc4, 0x74, 0x43,
0x6c, 0x1f, 0x93, 0x77, 0xdc, 0xce, 0x20, 0x8c,
0x99, 0x5f, 0x44, 0x01, 0xf5, 0x1e, 0x87, 0x5e,
0x61, 0x2c, 0x4b, 0x1d, 0x81, 0x15, 0xf4, 0x23,
0xd6, 0xea, 0xe1, 0x67, 0xf1, 0x7f, 0xfe, 0xda,
0x3c, 0x07, 0x53, 0x6a, 0x84, 0x9c, 0xcb, 0x02,
0x83, 0x33, 0xdd, 0x35, 0xe2, 0x59, 0x5a, 0x98,
0xa5, 0x92, 0x64, 0x04, 0x06, 0x10, 0x4d, 0x1c,
0x97, 0x08, 0x31, 0xee, 0xab, 0x05, 0xaf, 0x79,
0xa0, 0x18, 0x46, 0x6d, 0xfc, 0x89, 0xd4, 0xc7,
0xff, 0xf0, 0xcf, 0x42, 0x91, 0xf8, 0x68, 0x0a,
0x65, 0x8e, 0xb6, 0xfd, 0xc3, 0xef, 0x78, 0x4c,
0xcc, 0x9e, 0x30, 0x2e, 0xbc, 0x0b, 0x54, 0x1a,
0xa6, 0xbb, 0x26, 0x80, 0x48, 0x94, 0x32, 0x7d,
0xa7, 0x3f, 0xae, 0x22, 0x3d, 0x66, 0xaa, 0xf6,
0x00, 0x5d, 0xbd, 0x4a, 0xe0, 0x3b, 0xb4, 0x17,
0x8b, 0x9f, 0x76, 0xb0, 0x24, 0x9a, 0x25, 0x63,
0xdb, 0xeb, 0x7a, 0x3e, 0x5c, 0xb3, 0xb1, 0x29,
0xf2, 0xca, 0x58, 0x6e, 0xd8, 0xa8, 0x2f, 0x75,
0xdf, 0x14, 0xfb, 0x13, 0x49, 0x88, 0xb2, 0xec,
0xe4, 0x34, 0x2d, 0x96, 0xc6, 0x3a, 0xed, 0x95,
0x0e, 0xe5, 0x85, 0x6b, 0x40, 0x21, 0x9b, 0x09,
0x19, 0x2b, 0x52, 0xde, 0x45, 0xa3, 0xfa, 0x51,
0xc2, 0xb5, 0xd1, 0x90, 0xb9, 0xf3, 0x37, 0xc1,
0x0d, 0xba, 0x41, 0x11, 0x38, 0x7b, 0xbe, 0xd0,
0xd5, 0x69, 0x36, 0xc8, 0x62, 0x1b, 0x82, 0x8f
}
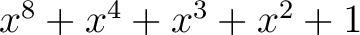
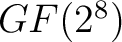
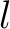
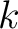
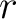
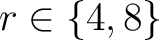
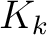
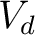
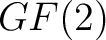
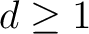


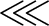

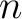
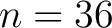
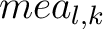
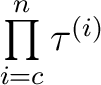
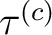
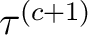
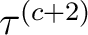
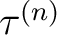
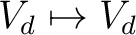
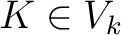
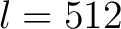
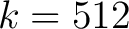
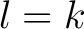
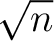
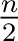
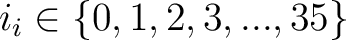
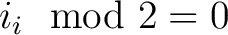
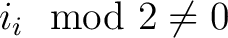
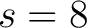
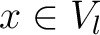
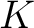
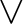
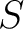
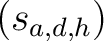
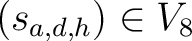
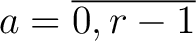
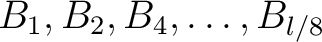
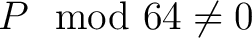
![[*]](footnote.png)
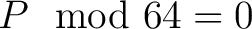
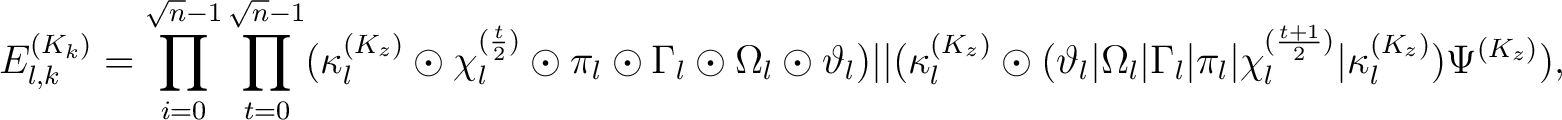
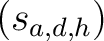
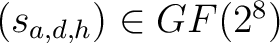
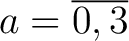
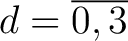
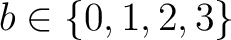
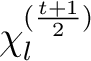
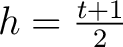
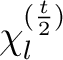
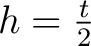
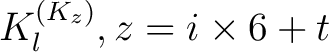
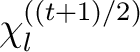
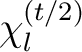
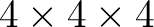
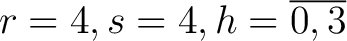
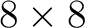
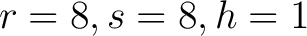
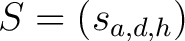
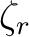
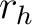
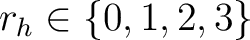
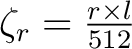
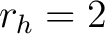
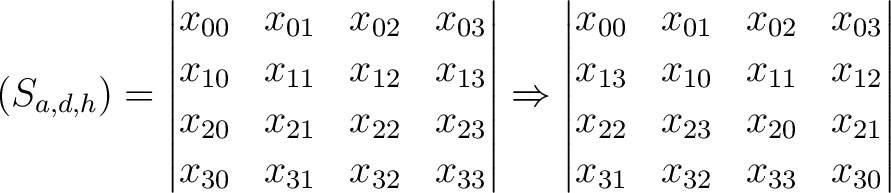
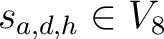
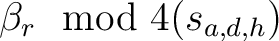
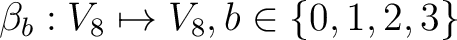
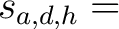
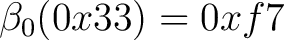
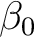
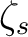
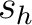
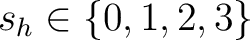
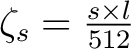
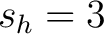
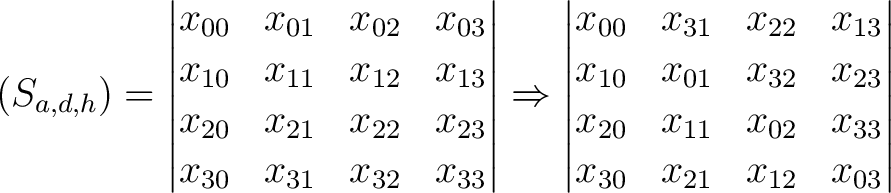
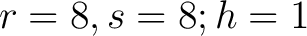
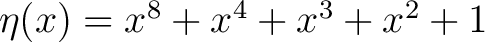
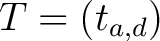
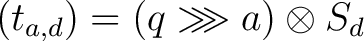

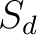
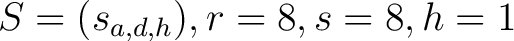
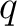
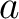
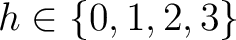
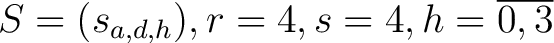
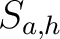
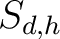
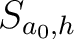
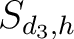
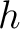
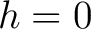
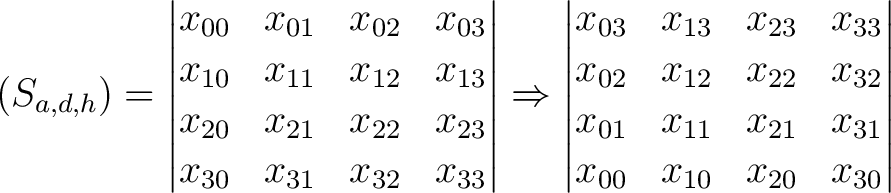
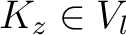
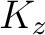
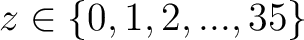
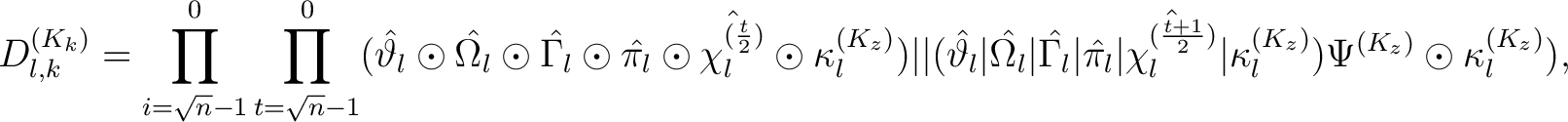
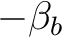
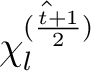
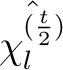
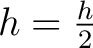
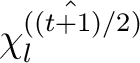
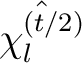
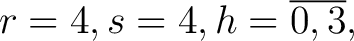
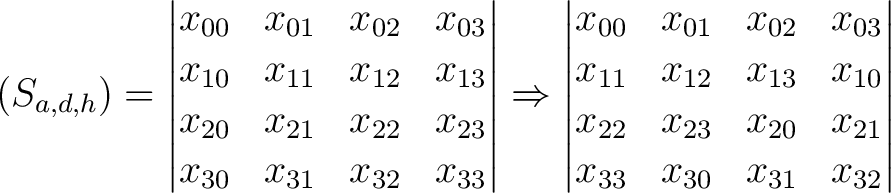
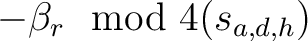
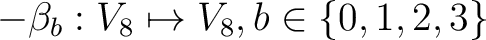
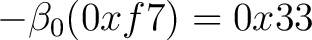
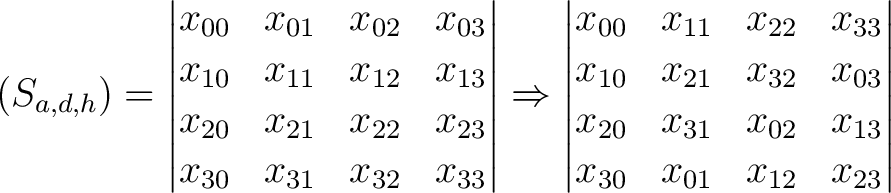
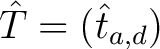
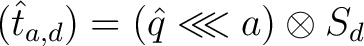

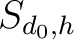
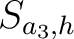
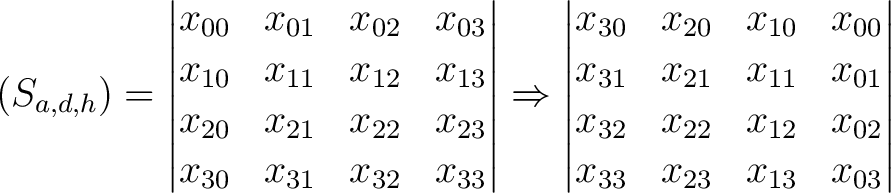
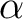
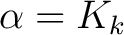
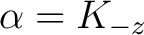
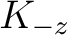
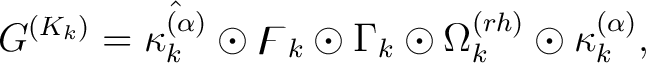
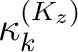
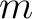
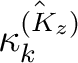
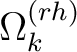
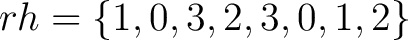
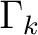
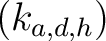
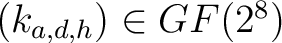
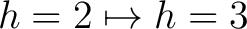
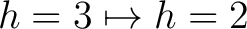
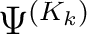
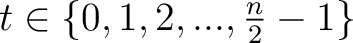
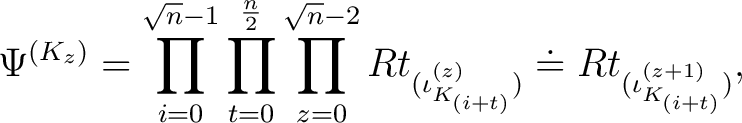
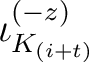
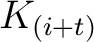
![$-y \in K_{[-z]}$](img189.png)